Last updated July 4, 2025
Since I've gotted interested in math, I've realized that despite doing well in math classes throughout middle and high school, there was a lot that I learned how to do but didn't understand how it works or why it matters. I've been going through problems on Alcumus to find out which concepts those are, and the first one I've run into is exponents.
Exponents as multiplication
You've probably heard at some point that \(b^x\) means to multiply \(b\) by itself \(x\) times, which works in many cases:
\[\begin{split} 7^3 = 7 \times 7 \times 7 = 343 \\ 2.5^4 = 2.5 \times 2.5 \times\ 2.5 \times 2.5 = 39.0625 \\ \text{etc.} \end{split}\]
Specifically, it works as long as \(x\) is a positive whole number.
Exponential growth
In other cases, this definition doesn't help as much. How would you multiply a number by itself 0.46 times or -3 times? Why would multiplying something by itself zero times equal 1? To understand how these kinds of exponents work, let's graph an exponential function:
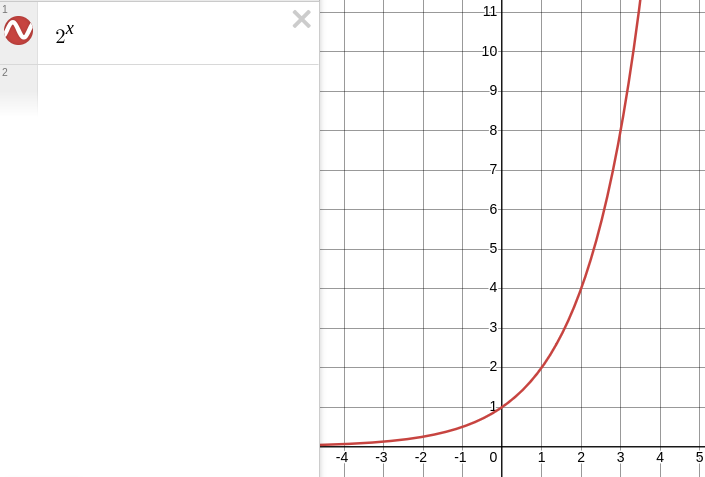
If the x axis represents time, then the y axis represents something that doubles every unit of time (second, day, year, etc.) Let's say it's the mass in milligrams of a colony of bacteria, which doubles every day. We know that \(2^1 = 2\), \(2^2 = 4\), \(2^3 = 16\), and so on. In this example, that means there's \(2 \text{mg}\) of bacteria after 1 day, \(4 \text{mg}\) after 2 days, and \(16 \text{mg}\) after 3 days.
Why \(\boldsymbol{b^{-x} = \frac{1}{b^x}}\)
We already know how to find the bacteria's mass any whole number of days after you started measuring it. How much did it weigh the day before? We know its mass doubles every day; if it weighed \(2 \text{mg}\) after 1 day, it must have weighed half of that the day before, half of that the day before that, and so on. Thus, we find it weighed \(2 \times \frac{1}{2} = 1 \text{mg}\) the day you first weighed the bacteria (at \(x = 0\)) and \(1 \times \frac{1}{2} = 0.5 \text{mg}\) the day before that. Just as a positive \(x\) represents the number of days after the first measurement, a negative \(x\) represents the number of days before. \(2^x\) doubles every time you increase \(x\) by 1, and halves every time you decrease it by \(1\).
Why \(\boldsymbol{b^0 = 1}\)
The bacteria wouldn't have necessarily weighed \(1 \text{mg}\) when you started, so why does \(b^0\) always equal 1? If it had a different mass when you started, say \(5 \text{mg}\), then it wouldn't be \(2 \text{mg}\) after 1 day either, it would be 2 times its initial amount; \(5 \times 2^1 = 10\). Since its inital mass was \(5 \text{mg}\), it follows that \(5 \times 2^0 = 5\), and \(2^0\) must equal 1. \(b^x\) represents the factor by which a value has grown from its initial amount.
When \(\boldsymbol{x}\) isn't a whole number
We can assume the mass of bacteria doesn't spontaneously double at the end of each day, it gradually grows throughout the day. How would we find what its mass was part of the way through a day? You may have learned the rule that \(b^\frac{m}{n} = \sqrt[n]{b^m}\).
Orders of magnitude
The digits in a number each have a place value. We can assign each place value an index telling us its distance from the ones place.

If you write a number in scientific notation, this highlights its order of magnitude. 72000 has its most significant digit at index 5 and would be written as \(7.2 \times 10^5\), \(7.2 \times 10^-5\) would have its most significant digit at index -5: 0.000072.
More on bases and place values
You can expand a number by multiplying each digit by \(10^n\), where \(n\) is the digit's index. \(12345.678\) can be expanded as such:
\[1(10^4) + 2(10^3) + 3(10^2) + 4(10^1) + 5(10^0) + 6(10^-1) + 7(10^-2) + 8(10^-3)\]
Raising 10 to different powers like this is the foundation of the base 10 number system, and using a base besides 10 you can form other number systems. For example, the binary number \(10101001\) can be expanded and converted to base 10:
\[\begin{split} 10101001_\text{base 2} &= 1(2^7) + 0(2^6) + 1(2^5) + 0(2^4) + 1(2^3) + 0(2^2) + 0(2^1) + 1(2^0) \\ &=2^7 + 2^5 + 2^3 + 2^0 \\ &= 128 + 32 + 8 + 1 \\ &= 169_\text{base 10} \end{split}\]
(The base doesn't even have to be a whole number. This seems to be relevant mainly in pure math, but apparently has applications in analog-to-digital signal conversion? I am not going to pretend to understand how that works though.)